ELECTRÓNICA DIGITAL
Sección SI.
sábado, 24 de diciembre de 2016
Este blog persigue una finalidad educativa, la cual radica en la exploración de conocimientos relacionados a dos temáticas de la Electrónica Digital, como lo son los Circuitos Combinacionales y los Circuitos Secuenciales.
De esta manera, en él se reflejan diversos aspectos básicos entre los que se pueden destacar: definiciones, clasificaciones, características, simbología, entre otros; aunado a una serie de ejercicios donde se aplica la teoría previamente explicada.
Este blog también cuenta con un apartado dedicado a una serie de videos complementarios que ahondan un poco más en las temáticas tratadas.
VIDEOS SOBRE CIRCUITOS COMBINACIONALES Y SECUENCIALES
SECCIÓN TEÓRICA
Introducción a los Circuitos Combinacionales
Diferencia entre Circuitos Combinacionales y Circuitos Secuenciales
Resumen sobre los Flip-flops
SECCIÓN PRÁCTICA
Mapas de Karnaugh
Ejercicio sobre Circuitos Combinacionales
Ejercicio de Flip-flop D
Ejercicio de Flip-flop JK
Ejercicio de Flip-flop T
EJERCICIOS DE CIRCUITOS SECUENCIALES
Ejercicio 1. Análisis de un circuito secuencial
Paso 1: Se obtienen las ecuaciones de excitación, identificando lo que hay en las entradas de los flip-flops.
Paso 2: Se escriben las ecuaciones de estado siguiente y salidas.
Paso 3: Se elabora la tabla de estado siguiente y salidas.
Paso 4: Se construye el diagrama de estado con la información de la tabla anterior.
Simplificando, se obtiene una expresión booleana de J1K1 J2K2:
De esta manera, el funcionamiento del diagrama será el siguiente:
Paso 2. Construcción de la tabla de estados
Paso 1: Se obtienen las ecuaciones de excitación, identificando lo que hay en las entradas de los flip-flops.
D0 = Cnt ' Q0 + Cnt Q'0
D1 = Cnt ' Q1 + Cnt Q1 ' Q0 + Cnt Q1 Q'0
D1 = Cnt ' Q1 + Cnt Q1 ' Q0 + Cnt Q1 Q'0
Paso 2: Se escriben las ecuaciones de estado siguiente y salidas.
Q0 (sig) = D0 = Cnt ' Q0 + Cnt Q'0
Q1 (sig) = D1 = Cnt ' Q1 + Cnt Q1 ' Q0 + Cnt Q1 Q'0
Paso 3: Se elabora la tabla de estado siguiente y salidas.
Estado actual
|
|
Q1
|
Q0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
Estado siguiente
|
|
Q1 (sig)
|
Q0 (sig)
|
Cnt = 0
|
Cnt = 1
|
0 0
|
0 1
|
0 1
|
1 0
|
1 0
|
1 1
|
1 1
|
0 0
|
Paso 4: Se construye el diagrama de estado con la información de la tabla anterior.
Ejercicio 2. Diseño de un circuito secuencial síncrono con biestables
Se parte del siguiente diagrama de flujo:
Como no existen salidas, se supone que las salidas de los flip-flops son las salidas del circuito.
La tabla de transición resulta:
| Q2 Q1 |
| 00 |
| 01 |
| 11 |
| 10 |
| X | ||
| 0 | 1 | |
| 00 | 01 | |
| 10 | 01 | |
| 11 | 00 | |
| 10 | 11 | |
Como existen dos variables de estado interno Q2 Q1, se necesitan dos elementos de memoria (dos flip-flop). El diseño será realizado con biestables JK, por lo que para cada uno de los biestables se debe deducir la entrada J y la entrada K, funciones que pueden realizarse utilizando puertas básicas o dispositivos MSI.
Se construye la tabla de estados de la siguiente manera:
Entrada
|
X
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
| Estado presente | ||
Q2
|
Q1
|
|
0
|
0
|
|
0
|
1
|
|
1
|
0
|
|
1
|
1
|
|
0
|
0
|
|
0
|
1
|
|
1
|
0
|
|
1
|
1
|
|
| Estado futuro | ||
Q2
|
Q1
|
|
0
|
0
|
|
1
|
0
|
|
1
|
0
|
|
1
|
1
|
|
0
|
1
|
|
0
|
1
|
|
1
|
1
|
|
0
|
0
| |
| Entradas biestables | |||||||
| J2 | K2 | J1 | K1 | ||||
| 0 | X | 0 | X | ||||
| 1 | X | X | 1 | ||||
| X | 0 | 0 | X | ||||
| X | 0 | X | 0 | ||||
| 0 | X | 1 | X | ||||
| 0 | X | X | 0 | ||||
| X | 0 | 1 | X | ||||
| X | 1 | X | 1 | ||||
Simplificando, se obtiene una expresión booleana de J1K1 J2K2:
J2 = Q1X'
K2 = Q1X
J1 = X
K1 = Q2'X' + Q2X
El circuito quedaría de la siguiente manera:
Ejercicio 3. Diseño de un circuito secuencial
El sistema de apertura de una caja fuerte está compuesto por dos teclas (A y B), un circuito secuencial a diseñar y un temporizador que mantiene la caja fuerte abierta durante 5 minutos cuando recibe un nivel lógico 1 desde el circuito secuencial. Este temporizador vuelve a cerrar la caja fuerte pasado dicho tiempo, independientemente del circuito secuencial.
Cuando se pulsa la tecla A, se produce un nivel lógico 1 que entra al circuito secuencial, mientras que cuando se pulsa la tecla B, se produce un nivel lógico 0 de entrada al circuito a diseñar. Mientras no se pulse ninguna tecla, no se genera ningún nivel lógico de entrada al circuito secuencial.
Para abrir la caja fuerte, la combinación secreta es: pulsar dos veces seguidas la tecla A, a continuación pulsar una vez la tecla B, y finalmente pulsar una vez la tecla A. Si se hace de esta manera, el circuito secuencial dará una salida a nivel lógico 1, que actuará sobre el temporizador, permitiendo la apertura de la caja fuerte durante 5 minutos. Si en cualquier momento se introdujera un error al pulsar la secuencia secreta, en el siguiente ciclo de reloj todos los biestables se pondrán a cero (el sistema pasará al estado inicial), y la secuencia debe volver a introducirse desde el principio.
a) Dibuje el diagrama de estados, explicando claramente en qué consiste cada estado.
b) Implemente el circuito secuencial a diseñar utilizando biestables JK y las puertas necesarias.
Solución
Paso 1. Indicar las especificaciones al diagrama de estados
En este caso, el diagrama de estados debe ser capaz de reconocer la combinación de entrada 1101. Se parte de un estado inicial en el que se espera la introducción del código. A continuación, se pasará a un nuevo estado cada vez que se reconozca correctamente el siguiente bit del código, mientras que si este no corresponde al código, se volverá al estado inicial y habrá que teclear todo el código de nuevo. El diagrama de estados será el siguiente:
Mientras que el significado de los estados será, por tanto, el de la siguiente tabla:
Estado
|
Definición
|
Q1
|
Q0
|
Q0
|
Estado inicial, no hay código.
|
0
|
0
|
Q1
|
Se ha recibido el primer 1.
|
0
|
1
|
Q2
|
Se han recibido dos 1 consecutivos.
|
1
|
0
|
Q3
|
Se ha recibido el 0 después de dos 1 consecutivos.
|
1
|
1
|
De esta manera, el funcionamiento del diagrama será el siguiente:
Inicialmente, se encuentra en el estado Q0. Mientras no se teclee un 1 se mantendrá en ese estado, puesto que la combinación válida es 1101. Cuando llegue el primer 1, el estado pasa a Q1, y si el siguiente bit es de nuevo un 1, se habrán reconocido los dos primeros correctamente, por lo que el siguiente estado será Q2. Sin embargo, si en lugar de un 1 se recibe un 0, la secuencia es incorrecta, y como resultado habrá que regresar a Q0 para que el código sea tecleado por completo de nuevo. Del mismo modo, al recibir un 0 estando en Q2 se pasará a Q3, puesto que se ha reconocido 110. Finalmente, si en la entrada Q3 es un 1, el código ha sido correcto, y por lo tanto la salida del circuito será 1 se volverá a . Si la entrada es un 0, entonces falló el último bit y, aunque se vuelva también a Q0, en este caso la salida del circuito será 0, puesto que el código fue erróneo.
Paso 2. Construcción de la tabla de estados
Tomando el diagrama de estados anterior debe generarse una tabla de estados, en la que a partir de las entradas y el estado actual se obtiene el siguiente estado, y en la que a partir de ambos y con ayuda de la tabla de excitación, se calcularán las entradas a los biestables, lo que hará que aparezca una función de salida (S) diferente del estado que almacenan los biestables.
E
|
Q1(t)
|
Q0(t)
|
Q1(t+1)
|
Q0(t+1)
|
J1
|
K1
|
J0
|
K0
|
S
|
0
|
0
|
0
|
0
|
0
|
0
|
X
|
0
|
X
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
X
|
X
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
X
|
0
|
1
|
X
|
0
|
0
|
1
|
1
|
0
|
0
|
X
|
1
|
X
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
X
|
1
|
X
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
X
|
X
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
X
|
1
|
0
|
X
|
0
|
1
|
1
|
1
|
0
|
0
|
X
|
1
|
X
|
1
|
1
|
Paso 3. Minimización de las funciones e implementación del circuito
Luego de simplificar a través del metodo de Karnaugh, se obtendrán las funciones de entrada a los biestables (J1, K1, J0, K0) para el cálculo del nuevo estado y la función de salida S.
J1 = E Q0
J0 = E XOR Q1
K1 = E + Q0
K0 = 1
S = E Q1 Q0
Ejercicio 4. Diseño de sistema secuencial síncrono
Se pretende diseñar un sistema secuencial síncrono con dos entradas (E1 y E0) y una salida S, usando biestables D, de manera que proporcione salida alta sólo cuando las dos entradas estén a nivel bajo, habiendo estado también a nivel bajo ambas entradas en el ciclo de reloj anterior. Las transiciones se producen en el flanco de bajada del reloj. En los restantes ciclos del reloj, la salida debe ser baja. Las señales de entrada son periódicas, con un período 5 veces superior al período de reloj. NOTA: No se producen todas las transiciones posibles.
a) Realizar el diagrama de transición de estados, definiendo y codificando los estados y las entradas.
b) Realizar la tabla de la verdad que resuelve el problema.
c) Encontrar el circuito
Paso 1. Realizar las especificaciones del diagrama de estados
Para determinar el número de estados necesarios, se debe tomar en cuenta en qué situaciones S toma los valores 0 y 1. En este caso, la salida S solamente se activará cuando ambas entradas (E1 y E0) tomen el valor 0, y además, tambien hayan sido 0 en el ciclo anterior. De esta manera, interesará diferenciar dos situaciones: aquella en la que las últimas entradas fueron 0 y otra en la que no se cumple esta condición. Si se da la primera, y las entradas vuelven a ser 0 de nuevo, S tomará el valor 1; y en cualquier otro caso, S será 0.
Para realizar el diagrama, hay que tener en cuenta que solo se dan las siguientes transiciones: Entrada E1E0 = 11 desde Q1, Entrada E1E0 = 00 desde Q1, Entrada E1E0 = 00 desde Q0 (la única que arroja de salida 1) y Entrada E1E0 = 10 desde Q0; lo que permite simplificar el diseño.
Estado
|
Definición
|
Q0
|
Entrada anterior = 00
|
Q1
|
Entrada anterior <> 00
|
El comportamiento queda reflejado en el diagrama de estados. Se puede observar como estando en el estado en el que las entradas anteriores fueron 00, mientras las entradas cumplan esa condición, la salida será 1. Si la condición anterior no se cumple, se cambia al estado Q1, puesto que E1 y E0 no fueron ambas 0. Por otra parte, estando en Q1 la salida siempre será 0, pues en el ciclo anterior las entradas no eran 0; y si lo fueran en el ciclo que se evalúa, se volvería de nuevo a Q0.
Paso 2. Construcción de la tabla de estados
Debe generarse con el diagrama de estados anterior. En ella, a partir de las entradas y el estado actual se obtendrá el siguiente estado, y en la que a partir de ambos, y con ayuda de la tabla de excitación, se calcularán las entradas al biestable D.
E1
|
E0
|
Q(t)
|
Q(t+1)
|
D
|
S
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
X
|
X
|
X
|
0
|
1
|
1
|
X
|
X
|
X
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
X
|
X
|
X
|
1
|
1
|
0
|
X
|
X
|
X
|
1
|
1
|
1
|
1
|
1
|
0
|
Paso 3. Minimización de las funciones e implementación del circuito
Se simplifica por Karnaugh para obtener la función de entrada al biestable D a utilizar para el cálculo del nuevo estado, y la función de salida S.
D = E1
S = Q' E1' = (Q + E1)'
jueves, 22 de diciembre de 2016
TABLAS DE EXCITACIÓN DE LOS CIRCUITOS SECUENCIALES
Flip-flop SR
Flip-flop JK
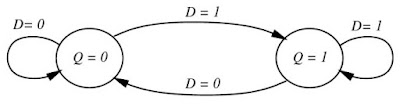
Flip-flop D
Flip-flop T
Q
|
Q (sig)
|
S
|
R
|
0
|
0
|
0
|
X
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
X
|
0
|
Flip-flop JK
Q
|
Q (sig)
|
J
|
K
|
0
|
0
|
0
|
X
|
0
|
1
|
1
|
X
|
1
|
0
|
X
|
1
|
1
|
1
|
X
|
0
|
Flip-flop D
Q
|
Q (sig)
|
D
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
Flip-flop T
Q
|
Q (sig)
|
T
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
ECUACIONES BOOLEANAS DE LOS CIRCUITOS SECUENCIALES
Flip-flop SR
Q (sig) = S + R'Q
SR = 0
|
Flip-flop JK
| Q (sig) = JQ' + K'Q |
Flip-flop D
| Q (sig) = D |
Flip-flop T
| Q (sig) = TQ' + T'Q |
Suscribirse a:
Comentarios (Atom)